요인 분석의 기초- PAF(요인분석)

출처 ; https://youtu.be/n3Sb6lQihPA?si=JQgscbUpi6TNw-XY

 

#상관관계 행렬은 분산 공분산 행렬을 표준화 한 것이므로 상관관계 행렬로 시작해도댐!

-> 상관관계 행렬이 매우 중요!!

#우리가 갖은 지표 점수(국어, 영어)를 종속 변수로 하고 나머지 지표 변수를 통해 유추

#SSE는 unique variance와 비슷하다고 본다. r스퀘어는 common variance와 비슷하다고 본다.

#분산을 r스퀘어로 대체 하는게 가능할까? 회귀분석과 비슷 하다고 본다.

#언어 능력은 변수로서 데이터로서 존재하지 않음 , 우리가 가진 지표 변수를 이용하여 한개의 지표 변수를 종속 변수로 하고 나머지 모든 변수를 없지만, 보이지 않지만 언어능력이라는 개념으로 보고 전부다 독립 변수로 놓고 그렇게 회귀분석으로 두고 ,,

#시작부터 우리는 설명되지 않은 분산을 버리고 시작했다는 것에 의미,, 

#어느 정도의 에러를 인정하고 시작하는 요인 분석은 주성분 분석과의 차이점!!

#주성분 분석은 총분산과 common variance 가 동일 했음

#요인분석은 1에서 빠진 좀 적어진 값을 unique variance 라고 본다.

#paf로 요인분석을 추출

#회귀분석으로 R스퀘어 값을 대체

#새로운 고유값과 고유 벡터를 구함

->새로운 factor matrix를 구함

#앞단계의 communality c0으로 0.96이 0.97이되고 이들을 뺴서 제곱하므로써 D를 계산

#고유값이 음수이면 factor가 0 이됨

#공통성이 0.96으로 시작 회귀분석으로 의 R스퀘어 값. comunality가 점점 커짐

#두변수와 요인의 상관계수의 제곱이 점점 증가

#국어,영어는 거의 98% 설명

#97.916으로 국어와 영어 점수의 분산을 설명.

#회귀분석을 이용해서 초기 값을 얻음->unique variance를 고려해야함

#국어 /영어 점수의 분산이 표준화된 분산은 0.979가 된다는 것

#초기 고유값은 주성분 분석의 파트와 동일->거기서 시작하여 마지막 itertation을 통해 얻은 고유값 1.958

주성분 분석일떄는 1.98,,

#1.958 나누기 2를 한게 %분산이됨. -> 변수가 두개이고 각각의 분산이 1인데 더해서 2가되므로 2로 나눔

-> 요인행렬의 0.99 두개를 합친것으로 보기도...

 

 

#unobeserve한 언어능력점수를 구하기!!

주성분 분석과 요인분석은 결과값이 비슷함

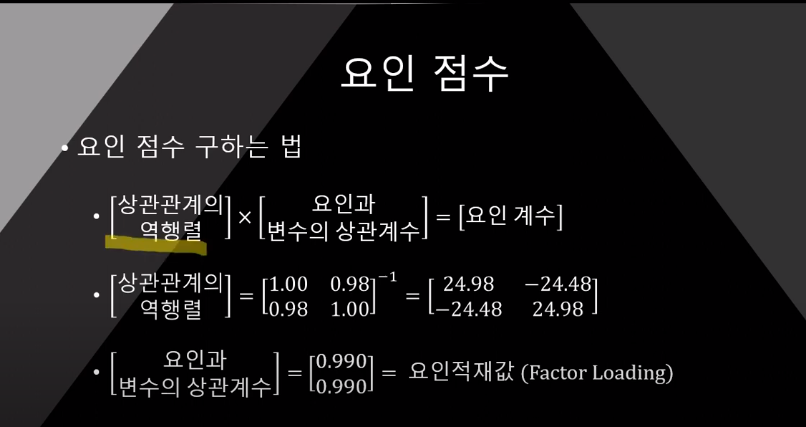
#그렇다면 언제 구분해서 사용하는가?

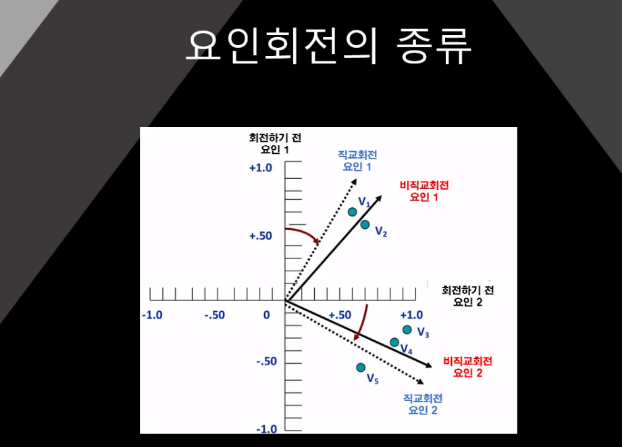
오른쪽은 주성분 분석을 통해 나타낸것 둘은 같은 데이터를 나타냄

#요인회전을 나타냄

#직교회전은 두개의 요인이 90도를 이룸, 상관관계가

0이라고 볼 수 있음

비직교회전은 90도를 이루지 않아도됨 또한 상관관계가 0이라고 볼 수 없음

#변수 1과 2는 첫번째 요인으로 묶이고 변수 3과 4는 두번째 요인으로 묶임

->변수의 이름을 보고 속성을 확인하고 요인1과 2의 이름을 그때가서 짓게 됨

-> 요인분석을 통해 요인이 도출되고 어떤요인이 어떤 변수에 묶이는지 확인하고 이름을 짓게됨

#베리멕스- 목표는 뽑아내고자하는 요인의 수를 최소화함

#직접오블리민-직교하지않는 요인들 , 요인이 서로간의 상관관계를 가지도록 허용

#가장중요한것은 직교냐 비직교냐!

#수입 교육정도 직업 부동산 가치는 개인의 사회경제상태로 묶일것이라고 가설을 세우고 요인분석을 할 것

집주변 공원의갯수 연간 범죄 발생수는 주변의 사회경제 상태와 묶일것이라고 가설을 세울 것

#표는 요인 적재량 을 나타냄, 팩터로딩값, 각가의 변수와 로딩간의 상관관계

숫자가 높을 수록 상관관계가 높은 것임. 수입은 0.63이므로 요인 1로 묶인다. 상관관계 계수 자체가 아주 높다라고 할 수 없는 교육 정도, 직업 부동산가치 들,.... 심지어 집주변 공원의 갯수와 연간 범죄 발생수도 요인 2와의 상관관계가 매우 작다. 심지어 연간 범죄 발생수는 요인 1이더크다. 0.20과 0.21은 요인1과 요인 2로 묶인다고 하기 어려움

#요인1과 요인 2사이의 상관관계가 0이되도록 하는 요인 회전으로  이상하게 요인이 비틀어짐

#개인의 사회경제상태와 주변의 사회경제 상태는 상관관계가 매우 높을 것.-> 당연한 상관관계가 강제로 0으로 바뀜으로 이상한 요인이 나오게 되는 것임

#앞의 예는 두개의 요인이 매우 상관관계가 높음

#실용적 동기와 즐거움적 동기에 대한 소비의 요인분석은 요인회전이 가능하다 왜냐하면 둘의 상관관계가 매우 낮거나 거의 없기 때문에

#요인분석은 상관관계가 높다면 직교회전 방법이 매우 위험하게됨. 일부러 우리가 가진 데이터를 강제로 변형시키기 때문

#그렇다면 회전방법을 쓰는 이유는뭐냐...

-애초에 연구자들이 전혀 상관관계가 없는 두가지요인을 전제로 설문지 개발을 해왔기에 자연히 회전방법을 써움

그러나, varimax를 쓰는 이유를 모른 채로 따라서 쓰게 되면 해석이안되는 경우가 많아진다.

->악화가 양화를 구축하는 상황이 발생

#varimax가 언제나 옳은 것은 아님