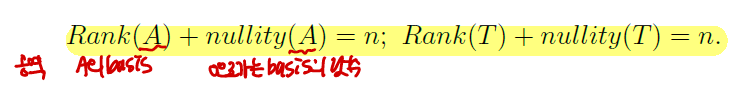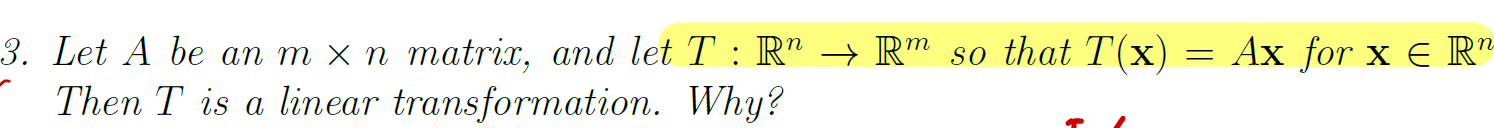story

4.1 projections the Gram-Schmidt orthogonalization procedure to obtain an orthogonal basis v, w ∈ Rn. Then the vector p in sp({w}) that is closest to v,, sp({w}) 에 포함된 벡터 p는 v와 제일 가깝다. vector p : the projection of v onto the subspace sp({w}) v = p + v − p and v − p ∈ sp({w})⊥ the decomposition v = p + v − p is unique the concept of projection onto a linear span of a vector to the general subspac..

2.3 Properties of Linear Transformations 1) Counterclockwise rotation T : R2 -> R2 는 a mapping which rotates a vector in the plane counterclockwisely by an angle θ 그러면 T는 linear transformation 이다. rotations T(v1) and T(v2) of two vectors v1 and v2은 길이와 두 벡터들의 각도를 보존한다. 그러므로 the rotations of tow vectors preserve the inner product, i.e., =. 그러므로 T(v1 + v2) = T(v1) + T(v2),T(rv) = rT (v)라 볼 수 있고 T는..

chapter 2.2 Rank and Nullity of a Matrix and a Linear Transformation three subspaces of Euclidean spaces associated with an m x n matrix: row space, column space and null space of the matrix ->이 세 개의 부분공간에 대한 관계를 알아보자. 그리고 A is an m x n matrix이고 linear transformation T(x) = Ax of Rn into Rm의 선형 변환이 존재. # null space of A/ column space of A/ dimension of he null space of A/ dimension of the range ..

chapter 2.1 Linear Transformations of Euclidean Spaces(선형변환함수) linear system of the form Ax = b with an m x n matrix A ->we could regard Ax as a function and view Ax = b as meaning that the function maps the vector x to the vector b. => f(x) = Ax with an m x n matrix A the domain(정의역) of this function should be a subset of Rn, the codomain(공역) be a subset of Rm f(av1 + bv2) = (av1 + bv2) = aAv1 ..