principal component anlysis in R(R에서 주성분 분석 실습)

#sample principal component analysis in R
#데이터 불러오기
sweat<-read.table("T5-1.DAT")
sweat
as.data.frame(sweat)
names(sweat)<-c("Sweat","Sodium","Potassium")
sweat

#covariance and correltation
s.cov<-cov(sweat)
s.cor<-cor(sweat)
s.cov

 
 
#eigenvalues and eigenvectors
eigen.cov<- eigen(s.cov)
eigen.cor<- eigen(s.cor)
eigen.cov
eigen.cor

고유값과 고유벡터 도출

 
 
#pca(covariance)
#sdev;the sd's of the pc(the square roots of the eigenvalues)
#standarddeviation-주성분요소들의 표준 편차들
#rotation; a matrix whose columns contain the eighenvectors
install.packages("mvtnorm")
library(mvtnorm) #먼저 깔아주기 prcomp 실행하기 위함
pca.cov<-prcomp(sweat)
pca.cov

summary(pca.cov)

 
->standard deviation: 개별 고유값의 크기(표준편차 제곱의 수치가 1이상인거 사용)
->proportion of variance: 분산 비율(주성분이 차지하는 비율)
->cumulative proportion:총변이에 대한 공헌도(80%이상인 것 까지...0.03정도의 손실 감수)
 
#pca results for correlation matrix
#pca(correlation)
pca.cor<-prcomp(sweat, center=T, scale=T)
pca.cor

summary(pca.cor)

 
#screeplot 그리기
screeplot(pca.cor,tyep='lines')

 
-> 수평축에 주성분을 놓고 수직축에 주성분에 해당되는 고유값을 연결. 그래프가 완만해지는 부분 이전이 바람직
 
 
#principal component regression analysis in R
 
1. 독립변수와 의존변수들을 표준화한다.
2.샘플 상관관계 메트릭스로부터 주성분 요소들을 얻는다.
3.일부 주성분 점수에 대해 표준화된 종속 변수를 회귀 분석한다.
4.원래 변수로 변환
 
#cement 를 가져오기-> y는 종속변수이다. x1~x7은 독립변수이다.
rm(list=ls())
par(mfrow=c(2,2))
cement<-read.csv("slump_test.data",header=T)
cement <- data.frame(X1=cement[,2],
                     X2=cement[,3],
                     X3=cement[,4],
                     X4=cement[,5],
                     X5=cement[,6],
                     X6=cement[,7],
                     X7=cement[,8],
                     Y=cement[,11])
cement
head(cement)

 
1) 독립변수들과 종속변수들을 표준화한다.

y.mean<-apply(cement[8],2,mean)
y.std<-apply(cement[8],2,sd)
scale.data<-as.data.frame(scale(cement))
head(round(scale.data,3))

 
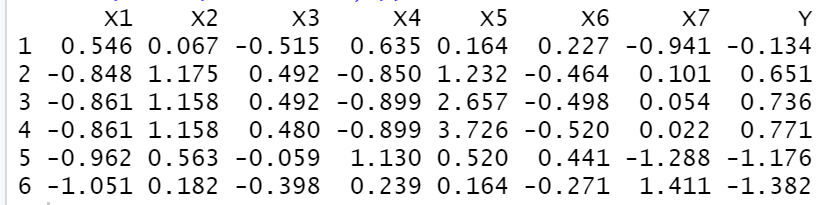
2) 표본 상관행렬에서 주성분 점수를 가져옴
par(mfrow=c(1,1))
data.pca<-prcomp(scale.data[1:7]) #독립변수만 주성분 분석을 함
plot(data.pca,type="1")
head(round(data.pca$x,3))

eigenCement<-eigen(cov(scale.data[1:7]))

eigenCement$values #주성분분석의 고유값들

eigenCement

 
3)표준화된 종속변수를 일부 주성분 점수에 대해 회귀분석
 
#pca score와 y를 사용해서 새로운 데이터 만들기
y<-scale(cement[,8])
pca.score<-data.pca$x
data<-cbind(as.data.frame(pca.score),y)
head(data)

#regression(pc1~pc4)
data.pcr<-glm(y~PC1+PC2+PC3+PC4,data=data)
summary(data.pcr)

 
 
*R2과 adj-R2을 계산하기
#coefficient of determination in pcr

one.vec<-rep(1,dim(pca.score)[1])
x.mat<-cbind(one.vec,pca.score[,(1:4)])
y.hat<-x.mat%*%as.vector(data.pcr$coefficients)
head(y.hat,3)

original.y.hat<-(y.hat*y.std)+y.mean
head(original.y.hat,3)
 

r <-sum((original.y.hat - y.mean)^2) / sum((cement[,8]+ - y.mean)^2)
ad.r <- 1-((dim(x.mat)[1]-1)*(1-r) / (dim(x.mat)[1]+ -dim(x.mat)[2]))
r
ad.r

 
 
<다른 방법은 모든 최소값들을 계산하는 대신 pls라는 패키지를 사용하는 것>
#use pcr code using correlation matrix
install.packages("pls")
library(pls)
scale.data<-as.data.frame(scale(cement))
pcr<-pcr(Y~.,data=scale.data,ncomp=4)
head(pcr$fitted.values,3)
 

ftn<-c(1:(103*3))
ftn

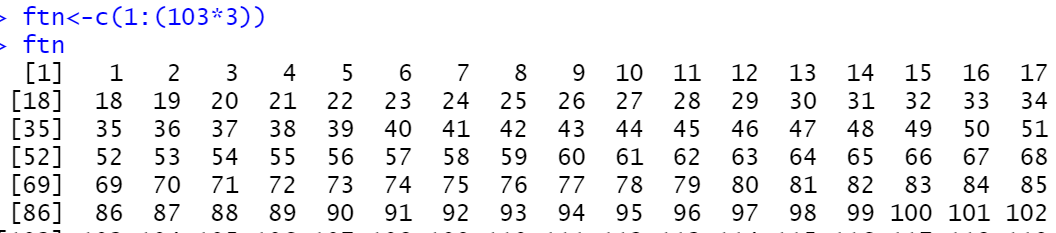
pcr.yhat<-as.vector(pcr$fitted.values[-ftn])
pcr.yhat

 
head(pcr.yhat,3)

#comparsion
#coefficient of determination
x.mat1<-cbind(one.vec,pcr$scores[,(1:4)])